
Figure 1: FA-18 Hornet breaking the sound barrier (7 July 1999).
This is an image of fighter jet travelling at the speed of sound (Mach 1). It was earlier speculated that sound moves fastest in denser materials such as diamond with speeds approaching 12,000 m/s. A team of researchers have found a new upper bound for the speed of sound, approximately 36,100 m/s, using dimensionless fundamental physical constants through experimenting on atomic hydrogen.
Source: ‘U.S. Navy footage/video’ (Wikimedia Commons)
The quest to quantify the speed of sound has long been taken up by physicists. These efforts date back to the 17th Century, when Pierre Gassendi estimated the speed of sound in air by approximating the time difference between detecting the flash of a gun and hearing its reception over a long displacement on a calm day and discovering it to be 478.4 m/s. More precise analyses were performed by the Academy of Sciences in 1738 that clocked the speed of sound to be 332 m/s. (Berg, 2019)
Recently, scientists from Queen Mary University of London, the University of Cambridge, and the Institute for High-Pressure Physics have made major strides by identifying the fastest speed (upper bound) of sound. (Trachenko, Monserrat, Pickard & Brazhkin, 2020)
In their paper published on 9th October 2020, on Sciences Advances, K. Trancheko, B. Monserrat, C.J Pickard and V. V. Brazhkin calculated the upper bound of the speed of sound to be 36,100 m/s (80753.4 miles per hour) by employing fundamental physical constants in their calculation. The first ones that they used were the fine structure constant – a measure of the strength of the electromagnetic force that governs how electrically charged elementary particles and photons react – and the proton-to-electron mass ratio (Curtis, 2019). Furthermore, because sound is dependent on its medium’s elasticity and vibrational properties, the team made use of the fact that the longitudinal speed of sound is dependent on the medium’s shear modulus and bulk modulus. They didn’t stop there. The researchers incorporated Rydberg’s energy – a physical constant relating to the electromagnetic spectra of an atom – and the Bohr Radius – a physical constant equal to the distance between the nucleus and the electron in a hydrogen atom (Curtis, 2019). They further resolved that the speed of sound in a medium is related to the square root of the medium’s atomic mass. (Trancheko et al., 2020).
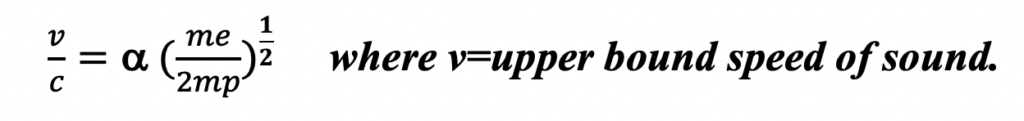
The scientists went on to test the validity of their equation on a variety of 36 elemental solid mediums, where they plotted a log-log plot of the speed of sound in that solid as a function of its atomic mass. Empirically, they ascertained that the speed of sound decreases when atomic mass increases, meaning that the upper bound of the speed of sound is to be found in solid hydrogen with strong metallic bonding (since it has the smallest atomic mass). Metallic hydrogen only exists at megabar pressures and is dynamically volatile at ambient pressure where molecular formation occurs. Thus, the team encountered an impediment; they could not source actual atomic hydrogen to test their hypothesis. Notwithstanding, they found a solution (admittedly imperfect) by conducting first-principles computations for I41/amd structure, the closest proxy they could find for atomic hydrogen, and performed the computations for this new structure in the pressure range of 250 to 1000GPa. They then graphed the speed of sound of this structure as a function of both pressure and density. These results agreed with the earlier prediction that sound should propagate at speeds up to 36,000 m/s. (Trancheko et al., 2020).
The implications of these results have already been perceived in the field of physics; for instance, this “new” upper bound of the speed of sound, which is twice the speed at which sound travels through very stiff diamond, has reconstructed how we view sound propagation. It sheds light on the usefulness of fundamental constants in defining the real-world behavior of matter and energy. In light of this, Vadim Brazhkin-one of the team of scientists in this experiment had already published a paper which revealed that the universal lower limit on viscosity is again denoted in terms of the proton-to-electron mass ratio and Planck’s constant. (Trachenko & Brazhkin, 2020). The use of the fine structure constant and proton-to-electron mass ratio have far-reaching connections too, among them being that these constants may govern nuclear reactions that lead to the formulation of primary biochemical elements like Carbon. (Trancheko et al., 2020).
This analysis, in conjunction with their already established data on bounds for viscosity and diffusivity, sheds light on the importance of finding the bounds of condensed matter phases. To further cement this conclusion, Professor Kostya Trachenko, Professor of Physics at Queen Mary asserted, “We believe the findings of this study could have further scientific applications by helping us to find and understand limits of different properties such as viscosity and thermal conductivity relevant for high-temperature superconductivity, quark-gluon plasma and even black hole physics.” (Rainey, 2020)
References
Berg, R. E. (2019, August 29). Measuring the speed of sound. Retrieved October 19, 2020, from https://www.britannica.com/science/acoustics/Measuring-the-speed-of-sound
NIST/ (2019, November 25). Fundamental Physical Constants. Retrieved October 20, 2020, from https://www.nist.gov/pml/fundamental-physical-constants
Rainey, C. J. (2020, October 12). MRI Scientists find upper limit for the speed of sound. Queen Mary University of London. Retrieved October 22, 2020, from https://www.materials.qmul.ac.uk/news/3738/mri-scientists-find-upper-limit-for-the-speed-of-sound
Trachenko, K., & Brazhkin, V. (2020, April 01). Minimal quantum viscosity from fundamental physical constants. Science Advances 6(17). Retrieved October 21, 2020, from https://advances.sciencemag.org/content/6/17/eaba3747
Trachenko, K., Monserrat, B., Pickard, C., & Brazhkin, V. (2020, October 01). Speed of sound from fundamental physical constants. Science Advances 6(41). Retrieved October 16, 2020, from https://advances.sciencemag.org/content/6/41/eabc8662
Related Posts
The Ubiquity of the Fibonacci Numbers
Figure 1: The Fibonacci Spiral. A shape that is derivative...
Read MoreNew ‘Drugless’ Approach to Killing Cancer Cells Shows Promise
Figure 1: Abstract Molecular Model Source: ShutterStock Researchers at Nanyang...
Read MoreCarbon-foam Light Sailing Could Take Us to the Stars in No Time
Figure 1: This is an image of LightSail 2, launched...
Read MoreCollins Kariuki



