
Figure 1: Dutch physicist Heike Kamerlingh Onnes. Onnes lay the foundations for the field of superconductivity. He was able to liquefy Helium down to a temperature of 0.9K (-272 °C), enabling him to discover superconductivity in mercury. The liquefication of Helium enabled him to discover superconductivity in mercury at a very low temperature which was previously unattainable. Subsequent tests of tin and lead showed that superconductivity was a property of numerous metals if they were cooled sufficiently (Ouboter, 1997; The Nobel Prize, n.d.)
Source: Wikimedia Commons
Superconductivity is defined by the complete disappearance of electrical resistance (the measure of the opposition to flow of electric current) of certain solids when they are cooled below a specific point known as the critical temperature.
Scientific studies of superconductivity began in 1911 with experiments on mercury in the laboratory of Dutch physicist Heike Kamerlingh Onnes. Onnes’ showed that when mercury was cooled to 4 Kelvin (-269 degrees Celsius), mercury’s electrical resistance ceased (Delft & Kes, 2011). The finding of zero electrical resistance is important because it could provide pathways to more efficient electrical applications, as a lot of energy tends to be lost due to electrical resistance. For instance, superconductors could be used national electric power lines and grid systems to minimize potential energy losses.
Most metallic superconductors (such as mercury and lead) are termed low-temperature superconductors since they only superconduct at temperatures below 73 Kelvin. Low-temperature superconductors require expensive cooling systems to maintain. On the other hand, materials with unconventionally high critical temperatures are aptly named high-temperature superconductors (HTS). HTS have critical temperatures above 77 Kelvin – the boiling point of nitrogen – and are comparatively easy to maintain using nitrogen as a coolant. HTS are mainly ceramics containing copper, oxygen, and rare-earth metals such as bismuth or thallium. HTS that contain Copper and Oxygen normally have very complex stoichiometries, that is, the ratios of the particular elements are often complex, for instance, Hg2Ba2Ca2Cu3O8 and Nd1.85Ce0.15CuO4 are examples of HTS with uncommon ratios. For this reason, they are sometimes called Unidentified Superconducting Objects (USOs). It is normally difficult to replicate superconductivity experiments in USOs as varying the oxygen content and heat drastically changes the HTS critical temperatures. Copper and oxygen HTS are crystalline in nature with the level of superconductivity highly dependent on the planar orientation of copper and oxygen atoms. (Ginsberg, 2018; OpenStax College ‘High-temperature Superconductors’ n.d.)
Despite the complicated science, investigations of superconductivity has gained traction. The discovery of the Meissner effect, which explores the magnetic properties of superconductors, by Walther Meissner and Robert Oschenfield sparked more interest in superconductivity. (Meissner & Oschenfield, 1933). The Meissner effect basically states that when a certain material is in a superconducting state (a state where there is imperceptible electrical resistance) it expels any externally applied magnetic field from penetrating it. The Meissner effect is essentially what makes magnets to levitate over superconducting materials (see figure 4) Another notable find was made by Bardeen, Cooper and Schrieffer. This theory for superconductivity, put forward by John Bardeen, Leon Cooper, and Robert Schrieffer in 1957 (Bardeen et al., 1957) seeks to explain superconductivity quantitatively through what are termed as Cooper Pairs (see figure 5) (Bardeen et al., 1957).
The joint achievement of J. Georg Bednorz and K. Alex Müller from IBM has also pushed the field forward. Through their years of testing ceramic compounds, they were able to develop, test and observe superconductivity in a brittle ceramic compound (BaxLa5−xCu5O5(3−y)) at 30 Kelvin (-243.15 degrees Celsius). Though far less than the conventional 73K threshold for attaining superconductivity, 30 was a very huge temperature and a big deal to experimental scientists in the 1970s and 1980s because before this time there had been no material superconductive at a temperature as high as 30 K (Bednorz & Muller, 1988).
Records in this field are being broken continuously with new, more complex superconductors being discovered. Moreover, more suitable candidates that display superconductivity are also being discovered. In a more recent paper published in Nature, researchers from the University of Rochester in New York discovered a carbonaceous Hydrogen sulphide, which currently holds the highest critical temperature at 15 degrees Celsius (Snider et al., 2020)
Cuprates have an important characteristic that leads to their superconducting nature: the presence of an electronic property called a single correlated d-band in the low energy spectrum (Isaacs & Wolverton, 2019). In the case of cuprates and iron compounds, technical difficulties such as getting the right ratios of particular elements of particular elements during the synthesis of crystals of these novel superconducting materials present hurdles, both in time and efficacy.
Currently, huge strides are being made to physically determine and actualize superconductors at even higher temperatures. Many elements and compounds like cuprates, graphene, metallic hydrogen, hydrates and hydrides are being tested for higher-temperature superconductivity.
Conductivity and Resistance
As mentioned earlier, electrical conductivity is the measure of the ease at which electric charge can pass through a material. Materials that conduct electricity are called conductors, and those which do not conduct electricity are called non-conductors or insulators (Lovatt & Shercliff, n.d.). Certain elements which lie between conducting and insulating phases are called semiconductors. Examples of semiconductors include silicon, germanium and gallium arsenide (Petruzzello, 2020). The conductivity of a particular material tells us how well electrical current flows through it. In most cases, the best conductors are metals. Examples of excellent metallic conductors include silver, gold, aluminum, copper, and iron; poor conductors include lead, tungsten, and bismuth.
Metals conduct electricity due to their structure. They are often composed of closely packed atoms that form crystal lattices with a high degree of symmetry. This symmetry leads to the high conductivity of metal because of the free-electron theory, which asserts that the atoms in the metallic lattice have lost their valence electrons – those in the outermost electron shell. The valence electrons are free to dissociate from their parent atoms and move around the lattice leading to the formation of the famous ‘sea’ of electrons. These electrons are the ones responsible for carrying charges around the metal and producing a flowing electric current. Insulators do not possess these highly mobile electrons and thus are not good conduits of electric current (Blaber & Shrestha, 2014).
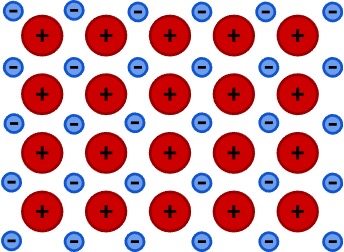
Figure 2: The positive charges represent cations (parent metal ions), and the negative charges represent free electrons within a metallic lattice. These free electrons can move easily throughout the lattice structure, making it easy for a metal to transport electric charge
Source: Wikimedia Commons
Electric current, even in metals, is not allowed to flow unimpeded. Electrical resistance is the measure of the opposition to the flow of current. Electrical resistance is more prominent in metals and transpires as a result of the crystalline metal lattice that makes conduction possible. When the mobile electrons in the lattice carry the charges through the conductor, they encounter their parent ions in the metal lattice (from which the electrons have broken free), which impede their motion. This, in turn, reduces the electrical conductivity of that particular conductor. The higher the resistance of a particular conductor, the lower the conductivity and vice versa.
Condensed matter physicists have examined the correlation between temperature and electrical resistance and have noted an almost proportional relationship between the two variables; that is, the increase in temperature results in an increase in resistance, but only up to a certain level (Elert, n.d.). 19th-century physicists thought that the plot of resistance vs. temperature would be linear for all temperatures. However, in 1908 when Heike Onnes first liquified Helium, he found that the electrical resistance of mercury completely disappeared at temperatures close to 3 Kelvin (Tretkoff, 2006).
Why the relationship between resistance and temperature? A higher temperature means that the parent ions in the metal have more kinetic energy, vibrating more extensively and engaging in a higher number of collisions with electrons (“New world encyclopedia,” n.d.). This is not entirely a negative phenomenon, as electrical resistance has certain technological applications (Gregersen, 2020). Because the tungsten filament in certain light bulbs has a high electrical resistance, the filament gets very hot and glows bright when electric current passes through it – it is resistance that allows buildings to be illuminated even in the dead of night (McGrayne et al., 2020).

Figure 3: Running current through a material with resistance results in energy loss. In this picture, energy is lost as heat and light
Source: Wikimedia Commons
According to Jordan Wirfs-Brock, a data journalist from University of Colorado, Boulder, about 69 trillion British Thermal Units (BTU) of energy was lost in 2013 just by transmitting electricity through the transmission and distribution grid in the USA, which utilizes reinforced aluminum conductor steel (ACSR), one of the best conductors of electricity (Wirfs-Brock, 2015; ElProCus, 2020). There doesn’t have to be this much energy loss. If the right materials are used, The wasted energy can be saved (African Development Bank Group, n.d.).

Figure 4: A transmission line connected to the National Grid System. National grid systems all over the world lose a lot of energy due to the electrical resistance of the cables carrying electrical current. A suitable superconductor could help reduce these energy losses
Source: Wikimedia Commons
Types of Superconductors and the Meissner Effect
The Meissner effect explores the relationship between different categories of superconductors and their response towards applied external magnetic fields. The Meissner effect is a phenomenon whereby, below its critical temperature, a superconductor expels externally applied magnetic fields that permeate it. This phenomenon depends on the type of superconductor in question (Diebner, 2016).
Diamagnetism is a phenomenon that causes materials to line up at right angles to a nonuniform magnetic field in which they are placed. It is prominent in materials such as rare gases (Gregersen et al., 2015). A type-I superconductor, also called a soft superconductor, will expel the external magnetic field completely when it is superconducting – it is then said to be in perfect diamagnetism. Examples of type-I conductors include tin, zinc, lead, etc. and are mostly pure metals. By contrast, a type-II superconductor, or a hard superconductor, only portrays a partial Meissner effect when external magnetic fields pass through certain regions. Niobium-titanium is an example of a type-II superconductor (Diebner, 2016).
Type-I superconductors do not maintain the non-permeated state at higher temperatures and therefore the Meissner effect in these superconductors is limited to lower temperatures. As a result, type-II superconductors are preferred and are widely used even in huge devices such as particle accelerators. Unfortunately, the mechanisms underlying this class of superconductors is currently not known and can only be conjectured. Understanding how these highly efficient type-II superconductors work will be crucial to help scientists solve some of the problems that block the efficacy of type-I superconductors (Hyperphysics, n.d.).
The Meissner effect, through the different types of superconductors, has important applications in the health and biomedical engineering sector. Magnetic Resonance Imaging (MRIs) scanners function by locating the precession (the slow rotation of the axis of an object around another axis due to exerted torques) of the magnetization of atomic nuclei within the human body. The greater the magnetization, the more efficient and clearer the MRI scans are. Very large superconducting magnets are used to generate enormous magnetic fields and enhance the magnetization of nuclei. The zero-resistance property of superconductors are utilized in MRIs. Zero resistance means that more current can flow, which in turn means that the magnetization effect is stronger. This is the chief reason why superconducting magnets are used in MRIs. If another material like a copper electromagnet was used, very large electrical resistance would be generated in the copper coils and would thus lead to energy loss through thermal dissipation and/or melting of the copper coils (Alloul et al., n.d.).
Particle colliders, like the Large Hadron Collider, also employ the use of superconducting magnets to allow particles to speed up inside the 27-km tunnel to near-light speeds without losing any energy (Gourlay, 2017). These superconducting magnets are especially important in guiding the particles through corners as they travel at high speeds.

Figure 5: Levitation of a magnet on top of a superconductor of cuprate type YBa2Cu3O7 cooled at -196°C. A magnet can levitate above a superconductor due to the Meissner effect. If this phenomenon can be harnessed on a large scale, it could mean a revolution for our transport sector as magnetic levitation trains could be made widely accessible
Source: Wikimedia Commons, Julien Bobroff and Frederic Bouquet
Finally, the Meissner effect is useful in that it allows for magnetic levitation (maglev) trains. Maglev trains use of superconducting magnets, which apart from creating their magnetic fields, also use the Meissner effect to levitate over the tracks over which they are laid. The non-permeability of the superconductors towards the magnetic field and the fact that magnetic poles repel is what makes maglev trains possible (Whyte, 2016).
Cooper Pairs and The Problem of Temperature
Going back to conductivity, we again take note of the crystalline lattice in metal conductors. The atoms in this metal lattice are always in random motion, vibrating around their average position. This random motion impedes the movement of electrons, which carry charges, and as a result reduces the amount of electric current that flows inside the conductor thus causing resistance (Galsin, 2002). Temperature has the most significant effect on these random vibrations and hence acts as an important factor in the conductivity of a material (Barron & Ashton, n.d.).
When the temperature is reduced close to absolute zero, the random motion of the atoms in the metal lattice almost comes to a halt and the vibration of the atoms about their mean position decreases (Delpierre & Sewell, 2005).
When an electron approaches the metal lattice, it encounters a multitude of positively charged atoms that have lost their valence electrons. By the laws of electrostatics, which states that unlike charges attract, the negatively charged electron and the positively charged atoms are attracted to each other. As the electron moves through the lattice, the surrounding positively charged particles are drawn near the electron to form an electron-phonon disturbance. This deformation moves through the lattice and becomes even more positively charged due to the conglomeration of the positive atoms around the first electron. When a second electron moves through the lattice, it is greatly attracted to the electron-phonon disturbance because it is more positively charged (Bardeen et al., 1957). The first and second electron then form what is known as a Cooper pair, which ranges from around 100 to 1000 atoms in length – this is known as the coherence length (Kadlin, 2005).
The connections that make a Cooper pair are relatively weak and would otherwise break when the conducting material is exposed to even higher temperatures. Thus, a very cool environment provided by liquid Helium is needed to support a Cooper pair (Hyperphysics, n.d.).
The number of Cooper pairs across the metal lattice multiples over time. Due to the Cooper pair’s vast length, they overlap to form many entanglements which strengthen their “weak” connections. Hence, the set of all the Cooper pairs in the system act as one large unit that is essentially unbreakable. If one of the Cooper pair connections are broken, the free electrons could just form another Cooper pair with other free electrons instantly and join back into the vast system of entanglement (Superconductivity, n.d.). The Cooper pairs then move through the conducting material unimpeded, mainly since the vibrations of the other positively charged atoms are at a minimum (Superconductivity, n.d.).

Figure 6: Cooper pairs within an atomic lattice. (Not to scale). Cooper pairs are pairs of electrons in a superconductor that are attractively bound and have equal and opposite momentum and spin (Merriam-Webster, n.d)
Source: Wikimedia Commons, Julien Bobroff and Frederic Bouquet
Fermions are subatomic particles, like electrons, that have odd angular momentum spins (e.g., ½, 3/2, 5/2, etc.) while bosons are subatomic particles with integer spins, (e.g., 1,2,3, etc.). Fermions and bosons are part of a larger umbrella of sub-atomic particles called quantons, which refers to particles that exhibit both wave and particle-like characteristics (Moore, 2003). What makes Cooper pairs interesting from a particle physics perspective is that they allow the “transformation” of a Fermion into a more advantageous boson. Electrons are fermions and must obey the Pauli exclusion principle, which states that no two quantons can share the same quantum state or energy level (Keilman & Garćia-Ripoli, 2008). However, this does not apply to bosons. When the electrons pair up into a Cooper pair, the two electrons act like a boson and can thus share the same quantum state. This bosonic characteristic of Cooper pairs has been tested by Samuelsson and Büttiker (de Llano et al., 2006). The bosonic properties of Cooper Pairs has the effect of minimizing the collisions that happen across the conducting material, allowing for zero resistance and thus the achievement of the superconductivity phenomena. Essentially, without Cooper pairs, superconductivity would not be possible. Furthermore, there has been experimental evidence supporting the BCS theory that cemented the notion of Cooper pairs as an integral part of superconductivity (Keilman & Garćia-Ripoli, 2008).

Figure 7: Historical plaque on the campus of the University of Illinois at Urbana-Champaign (UIUC), Urbana-Champaign commemorating John Bardeen’s role in developing a theory for superconductivity
Source: Wikimedia Commons
Despite this great feat, superconductivity is rendered impractical for real-life applications when the sub-zero temperature required is taken into account. Quantum computers that utilize superconductors, for example, need to be kept at very low temperatures. IBM’s supercomputers are kept at near absolute zero (0.015 K / -459.6430F / -273.1350C), a condition maintained by huge vats of liquified Helium (Fisher, 2019). The Large Hadron Collider, which uses superconducting magnets, is kept at a temperature of 1.9 Kelvin (Rossi, 2003). And the superconducting magnets used in magnetic levitating trains (maglevs) are currently kept at approximately 6 Kelvin (Whyte, 2016). The act of maintaining low temperature is quite an expensive one, and it makes superconductivity applications accessible only to huge companies and government-funded research.
Superconductivity in Cuprates.
Cuprates are compounds that consist of a layered alternating structure in which the two-dimensional superconducting compound Cu2O is infused with other layers of other metals or elements to act as electron/hole donors that stabilize the lattice. In most superconducting models involving cuprates, the superconducting activity occurs at the juncture between the oxide layers and those of the doped substance. The arrangement and layering patterns of the Cu2O layers can affect the temperature at which superconductivity is attained; the greater the number of layers, the higher the critical temperature.

Figure 8: A sample of a BSCCO crystal, a cuprate, which currently is one of the most practical high-temperature superconductors
Source: Wikimedia Commons
Unlike conventional superconductors whose superconductivity is based on electron-phonon interactions, superconductivity in cuprates depends on a more exotic form of electronic transmission involving electron-electron interactions. Most cuprates (which are Type 2 superconductors) allow magnetic penetration in quantized fluxes and can consequently sustain stronger magnetic fields (Diebner, 2016).
Because cuprates are made from multiple elements with a variety of physical and chemical properties, theoretical models to explain the mechanisms of superconductivity in cuprates have proven elusive. Currently, two theories exist, although neither is fully substantiated: the Weak coupling theory and the Interlayer coupling model. The former proposes that the unconventional superconductivity emerges as a result of antiferromagnetic spin fluctuations in a doped system, while the latter proposes that it emerges as an intrinsic self-enhancing BCS type superconductivity within a layered structure (Chakravarty et al., 1993; Monthoux et al., 1992). Further in-depth research is therefore needed to better understand the mechanisms of unconventional superconductivity.
Superconductivity in Graphene
Graphene is an allotrope (a different structural forms of a particular element) of carbon that consists of a single hexagonal layer of carbons atoms one atom-thick (see figure 8). In 2018, researchers made a subtle discovery about graphene. When two layers of atom-thick graphene are stacked together, they form a bi-layer that is twisted at an angle of 1.10 along its main axis. When a voltage is applied across this twisted matrix, the resulting increase in electron density morphs the graphene bilayer into a superconductor. Paradoxically, a marginal fluctuation in the electron density alters the graphene into an insulator that is impervious to electron flow. For this reason, the angle of twisting has memorably been referred to as the “magic angle.” Both the insulating and superconducting phases were attained at very low temperatures of approximately absolute zero, although under special circumstances, Twisted Bi-layer Graphene (TBG) can exhibit a critical temperature of up to 3 Kelvin (Cao et al., 2018).
To achieve the magic angle requires such dexterity that if thousands of samples are subjected to the mechanics of twistronics (manipulating the electronic properties of Two-dimensional layered structures through twisting them through small angles), only a few would emerge with superconducting ability. (Carr et al., 2016; Christos et al., 2020). This close transition between superconducting and insulating phases spurred a lot of interest among researchers, as it could potentially aid in the understanding of higher temperature superconducting mechanisms. The direct relationship also offers new insights into geometric topology and electrical conductivity in nature. Recently, researchers at Caltech were able to dope the graphene bi-layers with selenium and tungsten. The researchers achieved superconductivity at a relatively wider angle than to the magic angle and superconductivity was also stabilized since the insulator state was not triggered, even after varying the electron density (Arora et al., 2020).

Figure 9: A hexagonal layer of a one atom-thick graphene sheet
Source: Wikimedia Commons
Hydrogen superconductivity and the problem of pressure.
As early as 1968, scientists such as Neil Ashcroft proposed that if hydrogen were to be modified or converted into metal, it would portray high-temperature superconductivity (Ashcroft, 1968). Scientists further investigated this property within hydrogen and in particular hydrides molecules.
One of the reasons why hydrogen-rich compounds are good candidates for superconductive materials is because hydrogen allows for a higher degree of electron-phonon disturbance, which results in an increased number of Cooper pairs and hence increased flow of electrical current at zero resistance (Snider et al., 2020). Uncreased local disturbance also augments the Cooper pair bonds by strengthening them further. This reduces the chance of the quantum bonds between the pairs breaking, ensuring higher electrical current flow (Snider et al., 2020).
It is not enough, though, to only include hydrogen in the mix. Hydrides prove to be even more formidable candidates than pure metallic hydrogen when it comes to superconductivity. The more the number of hydrogen atoms in a particular compound, the greater the strength of the collective bonds and hence a higher chance of superconductivity occurring. As a result, many scientists have been experimenting with a wide array of hydrides to observe their critical temperatures and see if any exhibit high-temperature superconductivity (Huang et al., 2019).
One promising hydride is lanthanum hydride (H3S), which has attained superconductivity at 250 Kelvin or -23.15 degrees Celsius (Drozdov et al., 2019). Other “covalent super-hydrides” have been doped with different elements to induce the effect of stronger bonds that enhance the formations of even more Cooper pairs than normal hydrides (Pickard et al., 2020). An example of the latter includes carbonaceous super hydrides, which have been the most promising candidates thus far (Snider et al., 2020). Snider et al. (of the University of Rochester) used carbonaceous super hydrides and achieved superconductivity at almost 15 degrees Celsius (Snider et al., 2020).
Hydrogen is the lightest element and most abundant. It naturally exists as a molecular gas. So, in its molecular state, hydrogen is not of much use in conducting superconductivity experiments (Jolly, 2020). To make it useful for conductivity applications, molecular hydrogen must be converted into metallic hydrogen. The only way to metallize molecular hydrogen is through extreme pressure (Dias & Silvera, 2017).
In their initial superconductivity experiments, Eremets and his team of scientists from the Max Plank Institute for Chemistry investigated the superconductive properties of hydrogen at extreme pressures of around 440 Gpa (Eremets Group, n.d.). Comparatively, the pressure inside the earth’s core is around 360 Gpa (Evers, 2015). In Snider et al.’s experiments with carbonaceous super hydrides, the team investigated superconductivity at pressures around 275 Gpa. To do so, Snider et al. employed pocket-sized Diamond Anvil Cells (DACs), which condense their target hydrides into sizes on the order of micrometres. The research team was able to report superconductivity at maximum superconducting critical temperatures of about 15 degrees Celsius at around 267 Gigapascals. (Snider et al., 2020). To give another example, despite obtaining room temperature superconductivity, the gas H2S can only be made into a solid conductor at such high pressures — nearly 450 Giga pascals. This level of pressure can only be achieved in DACs and is unfeasible for practical applications in larger-scale models.
The extreme pressures at which superconductivity occurs has limited the efficacy of current superconductors, even though higher temperature superconductivity is being attained. A dilemma exists in that whatever benefit that may have be derived from newly discovered superconductors must be balanced with the high cost of maintaining them at a high pressure or low temperature state.
Conclusions
Superconductivity has the potential to transform the world as we know it. The prospect of utilizing high-temperature superconductors will prove useful towards solving the energy crisis by minimizing heat energy loss with suitable superconductors as electric transmission cables. The energy that is currently being lost could be used to power low-income communities all around the world.
Furthermore, The global race to construct quantum computers is dependent on efforts to find suitable superconductors. The transport sector could also be transformed if maglevs are able to operate at higher temperatures. Additionally, advancements in maintaining a proper Meissner effect in type-II superconductors could also prove useful in manufacturing maglevs. However, the field of condensed matter physics – which deals with superconductors – has a lot of research work to do before these practical achievements are realized.
On a wider scale, superconductors are still a long way from making big impacts on the world, despite having been discovered almost a century ago. Condensed matter physicists need to think of a way to offset the problems of extremely low temperatures and extremely high pressures to make the dream of high-temperature superconductivity feasible.
References
ACSR Conductor: Types, Properties and Its Advantages. (2020, August 9). ElProCus – Electronic Projects for Engineering Students. https://www.elprocus.com/what-is-an-acsr-conductor-types-and-its-advantages/
Alloul, H., Antoine, C., & Balibar, S. (n.d.). Magnetic Resonance Imagery [..Fr]. Supraconductivity. Retrieved March 8, 2021, from http://www.supraconductivite.fr/en/index.php?p=applications-medical-irm-more
Ashcroft, N. W. (1968). Metallic Hydrogen: A High-Temperature Superconductor? Physical Review Letters, 21(26), 1748–1749. https://doi.org/10.1103/PhysRevLett.21.1748
Bank, A. D. (2019, June 7). Light Up and Power Africa – A New Deal on Energy for Africa [Text]. African Development Bank – Building Today, a Better Africa Tomorrow; African Development Bank Group. https://www.afdb.org/en/the-high-5/light-up-and-power-africa-%E2%80%93-a-new-deal-on-energy-for-africa
Bardeen, J., Cooper, L., & Schrieffer, J. (1957). Theory of Superconductivity*. Physical Review, 108(5).
Barron, J., & Ashton, C. (n.d.). The Effect of Temperature on Conductivity Measurement. REAGECON, 3, 5.
BCS Superconductivity Theory. (n.d.). BCS Superconductivity Theory.
Bednorz, J., & Müller, K. (1988). Perovskite-type oxides The new approach to high-T, superconductivity. 60(3).
Blaber, M., & Shrestha, B. (2014, November 18). 6: Metals, Nonmetals, and Metalloids. Chemistry LibreTexts. https://chem.libretexts.org/Bookshelves/General_Chemistry/Map%3A_Chemistry_-_The_Central_Science_(Brown_et_al.)/07._Periodic_Properties_of_the_Elements/7.6%3A_Metals_Nonmetals_and_Metalloids
Carr, S., Massatt, D., Fang, S., Cazeaux, P., Luskin, M., & Kaxiras, E. (2016). Twistronics: Manipulating the Electronic Properties of Two-dimensional Layered Structures through their Twist Angle. Physical Review B, 95. https://doi.org/10.1103/PhysRevB.95.075420
Cooper Pairs and the BCS Theory of Superconductivity. (n.d.). Retrieved January 14, 2021, from http://hyperphysics.phy-astr.gsu.edu/hbase/Solids/coop.html
de Llano, M., Sevilla, F. J., & Tapia, S. (2006). Cooper pairs as bosons. International Journal of Modern Physics B, 20(20), 2931–2939. https://doi.org/10.1142/S0217979206034947
Delft, D. V., & Kes, P. (2011). The discovery of superconductivity. American Institute of Physics.
Delpierre, G., & Sewell, B. (2002, 2005). Temperature and Molecular Motion. https://www8.physics.utoronto.ca/~jharlow/teaching/everyday06/reading10.pdf
Dias, R. P., & Silvera, I. F. (2017). Observation of the Wigner-Huntington transition to metallic hydrogen. Science, 355(6326), 715–718. https://doi.org/10.1126/science.aal1579
Diebner, A. (2016, July 28). Meissner Effect. Engineering LibreTexts. https://eng.libretexts.org/Bookshelves/Materials_Science/Supplemental_Modules_(Materials_Science)/Magnetic_Properties/Meissner_Effect
Drozdov, A., Kong, P., Minkov, V., Kuzovnikov, M., Mozaffari, S., Balicas, L., Balakirev, F., Prakapenka, V., Greenberg, E., Knyazev, D., Tkacz, M., & Emerets, M. (2019). Superconductivity at 250 K in lanthanum hydride under high pressures. Nature. https://doi.org/10.1038/s41586-019-1201-8
Elert, G. (n.d.). Electric Resistance. The Physics Hypertextbook. Retrieved January 14, 2021, from https://physics.info/electric-resistance/
Emerson. (2010, January). Theory and Application of Conductivity. https://www.emerson.com/documents/automation/application-data-sheet-theory-application-of-conductivity-rosemount-en-68442.pdf
Eremets, M. I. (n.d.). Eremets Group. Retrieved January 14, 2021, from https://www.mpic.de/3538358/Eremets_Group
Evers, J. (2015, August 17). Core | National Geographic Society. https://www.nationalgeographic.org/encyclopedia/core/
Fisher, C. (2019, April 2). IBM | What is Quantum Computing? https://www.ibm.com/quantum-computing/learn/what-is-quantum-computing
Galsin, J. S. (2002). Physical Effects of Impurities in Metals. In J. S. Galsin, Impurity Scattering in Metallic Alloys (pp. 93–123). Springer US. https://doi.org/10.1007/978-1-4615-1241-7_5
Ginsberg, D. (2018, February 13). Superconductivity—Higher-temperature superconductivity. Encyclopedia Britannica. https://www.britannica.com/science/superconductivity
Gourlay, S. (2017, August 11). Powering the field forward. CERN Courier. https://cerncourier.com/a/powering-the-field-forward/
Gregersen, E. (2015, November 24). Diamagnetism | physics | Britannica. Britannica. https://www.britannica.com/science/diamagnetism
Gregersen, E. (2020, October 8). Resistance | electronics. Encyclopedia Britannica. https://www.britannica.com/technology/resistance-electronics
Huang, X., Wang, X., Duan, D., Sundqvist, B., Li, X., Huang, Y., Yu, H., Li, F., Zhou, Q., Liu, B., & Cui, T. (2019). High-temperature superconductivity in sulfur hydride evidenced by alternating-current magnetic susceptibility. https://doi.org/10.1093/nsr/nwz061
Isaacs, E. B., & Wolverton, C. (2019). Materials Informatics Approach to the Identification of One-Band Correlated Materials Analogous to the Cuprates. Physical Review X, 9(2), 021042. https://doi.org/10.1103/PhysRevX.9.021042
Jolly, W. (2020, June 1). Hydrogen | Properties, Uses, & Facts | Britannica. https://www.britannica.com/science/hydrogen
Kadin, A. M. (2007). Spatial Structure of the Cooper Pair. Journal of Superconductivity and Novel Magnetism, 20(4), 285–292. https://doi.org/10.1007/s10948-006-0198-z
Keilmann, T., & García-Ripoll, J. J. (2008). Dynamical Creation of Bosonic Cooper-Like Pairs. Physical Review Letters, 100(11), 110406. https://doi.org/10.1103/PhysRevLett.100.110406
Lovatt, A., & Shercliff, H. (n.d.). Conductivity. About Conductivity. Retrieved January 14, 2021, from https://www.lehigh.edu/~amb4/wbi/kwardlow/conductivity.htm
McGrayne, S., Suckling, E., Kashy, E., & Robinson, F. (2020, November 12). Electricity: Additional Information. Encyclopedia Britannica. https://www.britannica.com/science/electricity/additional-info
Meissner, W., & Ochsenfeld, R. (1933). Ein neuer Effekt bei Eintritt der Supraleitf�higkeit. Die Naturwissenschaften, 21(44), 787–788. https://doi.org/10.1007/BF01504252
Merriam-Webster. (n.d.). Cooper pair. In Merriam-Webster Dictionary.
Moore, T. (2003). Six Ideas That Shaped Physics (2nd ed.). http://www.physics.pomona.edu/sixideas/
OpenStax College. (n.d.). High-temperature Superconductors | Physics. Lumen Physics. Retrieved March 8, 2021, from https://courses.lumenlearning.com/physics/chapter/34-6-high-temperature-superconductors/
Ouboter, R. de B. (1997, March). Heike Kamerlingh Onnes’s Discovery of Superconductivity. https://web.njit.edu/~tyson/supercon_papers/Heike_Kamerlingh_Onnes_Discover.pdf
Petruzzello, M. (2020, November 5). Semiconductor | Definition, Examples, Types, Materials, Devices, & Facts | Britannica. https://www.britannica.com/science/semiconductor
Pickard, C. J., Errea, I., & Eremets, M. I. (2020). Superconducting Hydrides Under Pressure. Annual Review of Condensed Matter Physics, 11(1), 57–76. https://doi.org/10.1146/annurev-conmatphys-031218-013413
Rossi, L. (2003). The LHC Superconducting Magnets. EUROPEAN ORGANIZATION FOR NUCLEAR RESEARCH European Laboratory for Particle Physics, LHC Project Report 660, 6.
Snider, E., Dasenbrock-Gammon, N., McBride, R., Debessai, M., Vindana, H., Vencatasamy, K., Lawler, K. V., Salamat, A., & Dias, R. P. (2020). Room-temperature superconductivity in a carbonaceous sulfur hydride. Nature, 586(7829), 373–377. https://doi.org/10.1038/s41586-020-2801-z
Superconductivity. (n.d.). Retrieved January 14, 2021, from http://hyperphysics.phy-astr.gsu.edu/hbase/Solids/scond.html
The Nobel Prize. (n.d.). The Nobel Prize in Physics 1913: Heike Kamerlingh Onnes. NobelPrize.Org. Retrieved March 15, 2021, from https://www.nobelprize.org/prizes/physics/1913/onnes/facts/
Tretkoff, E. (2006, January). This Month in Physics History: January 1938: Discovery of Superfluidity. http://www.aps.org/publications/apsnews/200601/history.cfm
Whyte, C. (2016, June 14). How Maglev Works | Department of Energy. https://www.energy.gov/articles/how-maglev-works
Wirfs-Brock, J. (2015, November 6). Lost In Transmission: How Much Electricity Disappears Between A Power Plant And Your Plug? [..Org]. Inside Energy. http://insideenergy.org/2015/11/06/lost-in-transmission-how-much-electricity-disappears-between-a-power-plant-and-your-plug/
Related Posts
Possible Biosignature for Life Discovered on Venus
Figure 1: This is an image of Venus with its...
Read MoreCarbon-foam Light Sailing Could Take Us to the Stars in No Time
Figure 1: This is an image of LightSail 2, launched...
Read MorePCR: Captivation Through Replication
Executive Board Advisor: Nishi Jain Co-Authors: Vivek Babu, Collins Kariuki,...
Read MoreCollins Kariuki and Whitney Nicanor Mabwi



