Figure 1: The Fibonacci Spiral. A shape that is derivative of a special property of the Fibonacci Sequence, the Golden Ratio. The Fibonacci Spiral has a growth factor that is equivalent to the value of the Golden Ratio.
Source: Pixabay
Introduction
Throughout history, human beings have engrossed themselves with the unabating search for patterns in the physical world. One source of natural patterns is the Fibonacci sequence and the associated Fibonacci numbers. The Fibonacci sequence has proven to be ubiquitous, not only in the natural world but also in some structures within the human body like the cochlea (Pietsch et al., 2017).
The Fibonacci sequence, and the associated Fibonacci numbers, are defined by the following equation:
Fn = Fn-1 + Fn-2 for all n ≥ 3 where F1 = 1; F2 = 1
where Fn represents the nth Fibonacci number. The Fibonacci sequence can be written as {1,1,2,3,5,8,13,21,34,55,89,144,233…}.
The Golden Ratio is a concept that bears a strong connection to the Fibonacci Sequence. The term ‘Golden Ratio’ is often used interchangeably with the term ‘Golden Section,’ although some scholars have designated the term ‘Golden Section’ to be the reciprocal of the Golden Ratio. The Golden Ratio is believed to have come from Euclid, particularly from his famous book Elements, where he tried to solve a problem concerning the division of a line segment into two unequal parts and noted the size ratio of the resultant parts. This problem is more famously termed as “the problem of division of a line segment in extreme and mean ratio” (Benavoli et al., 2019).
This paper intends to highlight and elaborate on the origin and occurrences of the Fibonacci sequence and Fibonacci numbers, as well as the importance of the golden ratio not only in nature but also in scientific fields such as engineering.
History of the Fibonacci Sequence
The Fibonacci numbers are generally acknowledged to originate from Italian mathematician Leonardo Pisano, also known as Fibonacci. Fibonacci taught mathematics in Bugia, where his father, who was a trader, held a diplomatic post (Gies, 2020). During this time, Fibonacci travelled around the Mediterranean to gain expertise in ancient counting systems, with a focus on the Hindu-Arabic system which would later serve as the basis of his book, Liber Abaci (The Book of Calculations). In addition to the Fibonacci numbers, it also included the number Zephirum, which translates to zero (Ballieu, 2009). The number zero, originally serving as a place holder, would later serve as the foundation for the decimal system. The Liber abaci further incorporates the preceding discoveries of Pythagoras, Euclid, and Diophantus, including algorithmic methods acquired from Arab sources. The book, much like Euclid’s Elements, became an object of fascination and was widely reproduced and disseminated in Europe after Fibonacci finished writing it (Waerden & Baitak, 2019). Many people view the Liber Abaci as Fibonacci’s magnum opus because of the inclusion of not only pure mathematical elements such as the Hindu-Arabic system but also because of the introduction of applied mathematical elements such as cost and profit, barter, partnership, investment, allegation, and mensuration – the measuring of geometric magnitudes (Swetz, 2007).
One essential element of the Liber Abaci was that it proposed the Hindu-Arabic numerical system to the West. Fibonacci starts by declaring, “The nine Indian figures are: 9, 8, 7, 6, 5, 4, 3, 2, 1. With these figures, and with the sign 0… any number may be written” (Tesch, 2018).
The mechanical abacus, which had long been in use, was one of the most popular ways to perform calculations. It consisted of beads which slid along four wires. Each bead represents a unit. The prime disadvantage of this method of calculation was that it proved difficult to perform complex calculations, resulting in arithmetic errors. These errors could not be traced since the abacus does not provide a record of prior computations. Then came the Hindu-Arabic numerical system, which provided the solution to the problem which the abacists faced. This new method of counting was viewed as heresy because the abacus was so well suited for the counting of Roman numerals. This sparked a controversy among the abacists and the algorists – those who favored the new Hindu-Arabic numeral system (Allen, 2019).

Figure 2: A segment of the Liber Abaci (“The Book of Calculation”). Here, Fibonacci introduced the Hindu-Arabic numeral system that would later revolutionize Western arithmetic
Source: Wikimedia Commons
The Rabbit Problem
Perhaps one of the most well-known mathematical queries in history, the “Fibonacci Rabbit Problem.” finds its answer in the famous Fibonacci sequence. It posits:
“A certain man puts a pair of rabbits, one male and one female, in a place surrounded by a wall. How many pairs of rabbits can be produced from that pair in a year if it is supposed that every month each pair begets a new pair which from the second month on becomes productive?” (Allen, 2019).
This problem ultimately yields the Fibonacci Sequence as Fibonacci himself explained, in the Liber Abaci:
The initial pair of rabbits bear another pair in the first month and there will now be two pairs in the first month. Out of the two, only one of them bears another pair in the second month, and there shall be three pairs in the second month. Of these in one month, two pairs are pregnant, and two pairs of rabbits are born in the third month, and thus there are five pairs in the third month. Out of these three pairs are pregnant, and in the fourth month there are eight pairs, of which five pairs bear another five pairs; these are added to the eight pairs making thirteen pairs in the fifth month; of the thirteen pairs, eight pairs become pregnant, and thus there are in the sixth-month twenty-one pairs, and to these are added the thirteen pairs that are born in the seventh month; there will be thirty-four pairs in this month; to this are added the twenty-one pairs that are born in the eighth month; there will be fifty-five pairs in this month; to these are added the thirty-four pairs that are born in the ninth month; there will be eighty-nine pairs in this month; to these are added again the fifty-five pairs that are born in the tenth month; there will be 144 pairs in this month; to these are added again the 89 pairs that are born in the eleventh month; there will be 233 pairs in this month
To these are finally added the 144 pairs that are born in the last month; there will be 377 pairs, and these many pairs are produced from the above pair in the mentioned place at the end of the one year.
From the above, we can see that ultimately, the sequence below emerges:
{1,1,2,3,5,8,13,21,34,55,89,144,233…….}
And therefore, we shall get the general terms as:
F0 = 1. F1 = 1 F2 = 2 F3 = 3 F4 = 5 … Fn = Fn-1 + Fn-2
Of course, this is the famed Fibonacci sequence.
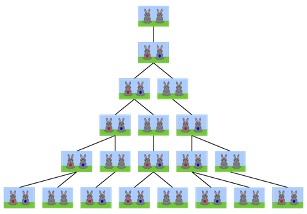
Figure 3: A pictograph of the famous “Rabbit problem.” Each pair of rabbits begets a new pair after a month
Source: Wikimedia Commons
The Golden Section
The Golden Section or Golden Ratio is a ratio which turns up in many arithmetic instances. Often denoted by the Greek letter phi, the Golden Section can be defined as follows:
Take a line segment and name it XY. Divide the line XY into two parts so that the ratio between the long ZY section and the short XZ section is proportional to the ratio between the whole line segment XY and the longer line section ZY.
Using Algebra, we can rewrite the above equation as follows:
And taking the positive root of the equation we eventually get to the irrational number we call the Golden Section (Benavoli et al., 2019).
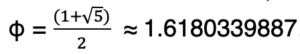
What does the Golden ratio have to do with the Fibonacci Sequence?
Revisiting our Fibonacci Sequence:
{1,1,2,3,5,8,13,21,34,55,89,144,233…….}.
And taking the limit of the ratio of consecutive terms of the above sequence (i.e. 144/89 = 1.6178, 233/144 = 1.6181, etc.), we find that the limit is equivalent to the Golden Ratio (Sinha, 2017).
The knowledge that the Fibonacci sequence converges to the Golden Ratio has inspired many to emulate this beautiful mathematical property that occurs in nature (see figure 4 below). For instance, this discovery has inspired a new field of study called architectural theory, whose main pillar is the Golden Section (Frings, 2002).
Properties of the Golden Section
Published in the Fibonacci Quarterly, Paul S. Brookman wrote a very succinct poem which he called “Constantly Mean.” It highlights some of the fundamental properties of the Golden Ratio.
The golden mean is quite absurd;
It’s not your ordinary surd.
If you invert it (this is fun!), You’ll get itself reduced by one;
But if increased by unity,
This yields its square, take it from me.
And the convergents, if you watch, Display the series Fibonacc’
In both their bottom and their top, that is, until you care to stop.
Since it belongs to F-root-five
Its value’s tedious to derive.
These properties are quite unique And make it something of a freak. Yes, one-point-six-one-eight-oh-three, You’re too irrational for me (Brukman, 1977).
From the amusing poem, we can see that the irrational number phi has some interesting properties: Its square is equal to φ+1, its reciprocal (sometimes referred to as the golden section) is equal to φ−1. Phi can be expressed as cascading fractions of 1 as shown in Figure 4:
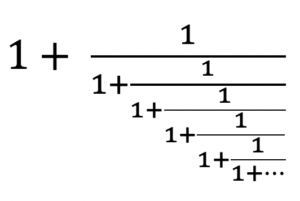
Figure 4: A property of the Golden Ratio. It can be expressed as an endless cascading fraction of one as shown above
Fibonacci In Nature
Another happy mathematical coincidence is the occurrence of the Fibonacci Numbers in nature. If you ever observe the flowers of certain plant species, you might notice that their petals occur in numbers that only emerge in the Fibonacci Sequence. For instance:
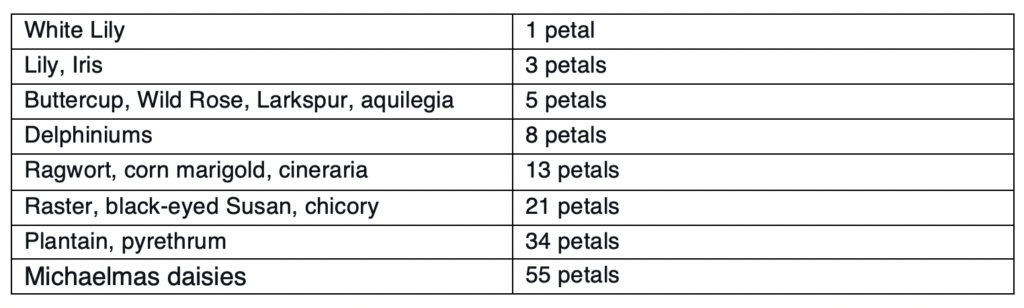
Figure 5: A table showing various flowers and the corresponding number of petals. The number of petals follow the Fibonacci Sequence pattern (Allen, 2018)
Taking a closer look at sunflower seed spirals and observing and count the clockwise and counterclockwise spirals that reach the outer edge – you will find the ubiquitous Fibonacci numbers. For instance, 34 and 55, or 55 and 89, or—with larger sunflowers—89 and 144 (Bohannon, 2017)

Figure 6: A sunflower. It has been shown that the number of seed spirals in a sunflower matches the Fibonacci numbers
Source: Wikimedia Commons
Architecture and the Fibonacci Numbers
The Fibonacci numbers not only occur in nature but also in architecture such as the Great Pyramid of Giza in Egypt. Taking the perimeter of the pyramid and dividing it by twice its height we find that the result is the Golden ratio. (Sinha, 2017)
The Golden section appears in many of the proportions of the Parthenon in Greece. The front elevation is built on the golden section (0.618 times as wide as it is tall). This ratio also is found in other parts of the building, including the width of the Parthenon’s front columns, and the height of the façade to its width (Meisner, 2013).
Conclusion
The Fibonacci Sequence is indeed a ubiquitous feature of the world. The Fibonacci sequence and Fibonacci numbers have laid the foundation for grasping how patterns emerge from everyday objects, and the field of recreational mathematics has definitely benefited from its universality. It takes a keen eye to notice how seemingly random objects follow an innate mathematical rule that subsists all around us. From sunflower seeds and petals (see figure 4) to the archetypal architecture found in Greece and Egypt, Fibonacci Numbers apply to almost everything.
References
Allen, S. (2019). Master Fibonacci: The Man Who Changed Math (1st ed.). Fibonacci Inc.
Ballieu, M. (2009, December 13). Fibonacci’s Liber Abaci (Book of Calculation). Math.Utah.Edu. https://www.math.utah.edu/~beebe/software/java/fibonacci/liber-abaci.html
Benavoli, A., Chisci, L., & Farina, A. (2009). Fibonacci sequence, golden section, Kalman filter and optimal control. Signal Processing, 89(8), 1483–1488. https://doi.org/10.1016/j.sigpro.2009.02.003
Bohannon, J., 2016, & Pm, 7:15. (2016, May 17). Sunflowers show complex Fibonacci sequences. Science | AAAS. https://www.sciencemag.org/news/2016/05/sunflowers-show-complex-fibonacci-sequences
Bruckman, P. (1977, October). Gaussian Fibonacci Numbers. Fibonacci Quarterly. https://www.fq.math.ca/Scanned/15-3/bruckman2.pdf
Friedenberg, J., & Silverman, G. (2006). Cognitive science: An introduction to the study of mind. Sage Publications.
Frings, M. (2002). The Golden Section in Architectural Theory. Nexus Network Journal, 4(1), 9–32. https://doi.org/10.1007/s00004-001-0002-0
Gies, F. (2020, April 12). Fibonacci | Biography & Facts. Encyclopedia Britannica. https://www.britannica.com/biography/Fibonacci
Meisner, G. (2013, January 20). The Parthenon and Phi, the Golden Ratio. The Golden Ratio: Phi, 1.618. https://www.goldennumber.net/parthenon-phi-golden-ratio/
Pietsch, M., Aguirre Dávila, L., Erfurt, P., Avci, E., Lenarz, T., & Kral, A. (2017). Spiral Form of the Human Cochlea Results from Spatial Constraints. Scientific Reports, 7(1), 7500. https://doi.org/10.1038/s41598-017-07795-4
Sinha, S. (2019). The Fibonacci Numbers and Its Amazing Applications. 6(9), 7–14.
Swetz, F. (2007, July). Fibonacci’s Liber Abaci | Mathematical Association of America. Mathematical Association of America. https://www.maa.org/press/periodicals/convergence/fibonaccis-liber-abaci
Taisbak, C., & Waerden, B. L. van der. (2019, August 2). Euclid | Biography, Contributions, & Facts. Encyclopedia Britannica. https://www.britannica.com/biography/Euclid-Greek-mathematician
Tesch, N. (2017, September 8). Hindu-Arabic numerals | History & Facts. Encyclopedia Britannica. https://www.britannica.com/topic/Hindu-Arabic-numerals
Related Posts
The Aesthetic Nature of Infinity and Repetition Seen in the Illustrations of M.C. Escher
Figure 1: “Tekening”, Sketch by M.C. Escher Image retrieved from...
Read MoreThe Pathway to Sonogenetics: Understanding the Mechanical Nature of the Ultrasound Stimulation Mechanism in C. Elegans
Figure 1: C. elegans in Agar under Microscope Magnification Source:...
Read MoreCollins Kariuki